티스토리 뷰
-선택 문제란?
n개의 숫자들 중에서 K번째로 작은 숫자를 찾는 문제이다.
최소 숫자를 k번 찾거나, 숫자들을 정렬한 후 k번째 숫자를 찾는 방법도 있지만, 각각 최악의 경우 O(kn)과 O(nlogn)의 수행 시간이 걸린다.
그래서 다른 방법으로, 정렬된 입력의 중간에 있는 숫자와 찾고자 하는 숫자를 비교함으로써, 입력을 2/1로 나눈 두 부분 중에서 한 부분만을 검색하는 방법이 있다.
퀵 정렬처럼 피봇을 무작위로 선택하고 한 부분을 정렬시킨다.
퀵 정렬과 다른 점은, 원하는 수가 속하는 '원하는 그룹'이 아니라면 정렬시킬 필요가 없다는 것이다.
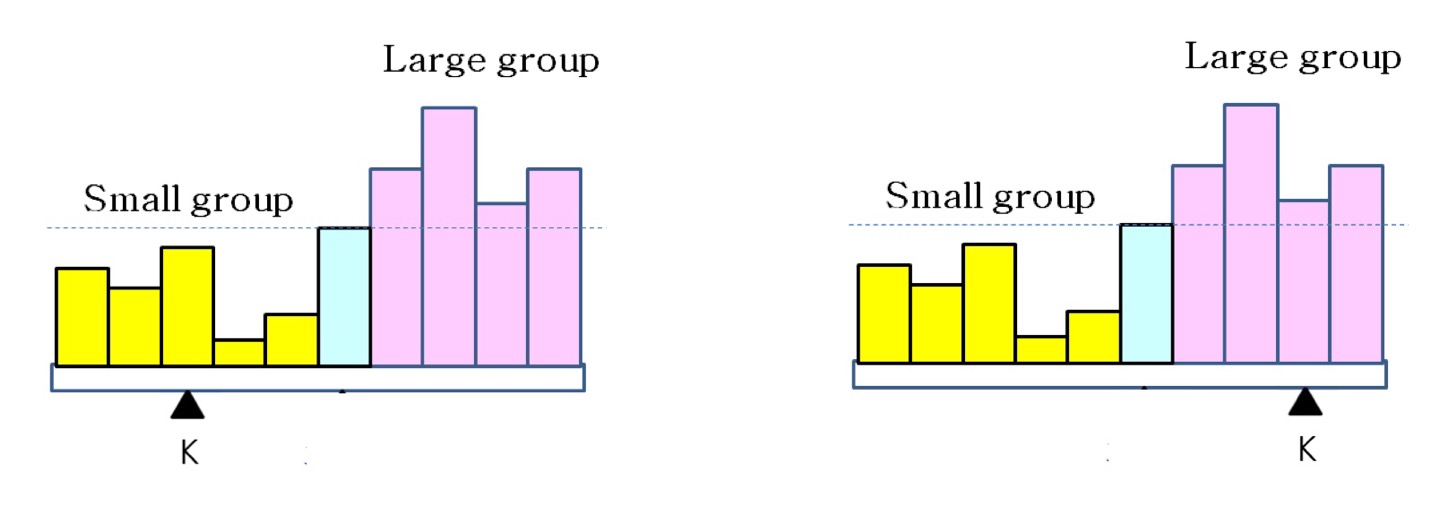
Small group은 피봇보다 작은 숫자의 그룹이고, Large group은 피봇보다 큰 숫자의 그룹
이 때 각 그룹의 크기를 알면, k번째 작은 숫자가 어느 그룹에 속해있는지를 알 수 있고 ,그 다음에는 그 그룹에서 몇 번째로 작은 숫자를 찾아야하는지를 알 수 있다.
-selection의 pseudo code
Selection(A, left, right, k)
입력: A[left]~A[right]와 k, 단, 1≤k≤|A|, |A|=right-left+1 출력: A[left]~A[right]에서 k 번째 작은 원소
1. 피봇을 A[left]~A[right]에서 랜덤하게 선택하고, 피봇과 A[left]의 자리를 바꾼 후, 피봇과 배열 의 각 원소를 비교하여 피봇보다 작은 숫자는 A[left]~A[p-1]로 옮기고, 피봇보다 큰 숫자는 A[p+1]~A[right]로 옮기며, 피봇은 A[p]에 놓는다.
2. S = (p-1)-left+1
3. if ( k ≤ S ) Selection(A, left, p-1, k) 4. else if ( k = S +1) return A[p]
5. else Selection(A, p+1, right, k-S-1)
// S = Small group의 크기 // Small group에서 찾기 // 피봇 = k번째 작은 숫자
// large group에서 찾기-Time Complexity
평균 경우 O(n)
-소스 코드
#include <stdio.h>
#include <stdlib.h>
#define SIZE 12
int Selection(int* A, int left, int right,int select) {
if (left < right) {//배열의 원소의 수가 2개 이상이면
int p, temp;
p = (left + right) / 2 ;//피봇 선택. 중간 원소의 인덱스로 선택했다.
temp = A[left];
A[left] = A[p];
A[p] = temp;//피봇을 A[left]와 자리를 바꾼다.
//A[left]와 A[p+1]~A[right]를 비교한다.
int i = left + 1;//배열의 원소를 하나씩 비교한다. i는 피봇보다 큰 값을 찾는다.
int j = right;//j는 피봇보다 작은 값을 찾는다.
while (i <= j) {//왼쪽과 오른쪽에서 시작한 i, j가 만나게 되면 비교 종료한다.
while (A[i] <= A[left] && i <= right)//피봇보다 작은 값이면 넘어감
i++;
while (A[j] >= A[left] && j > left)//피봇보다 큰 값이면 넘어감
j--;
if (i > j) {//i와 j가 엇갈리면 피봇 알맞은 위치로 바꿔줌
temp = A[j];
A[j] = A[left];
A[left] = temp;
}
else {//i번째 값과 j번째 값의 자리를 바꾼다.
temp = A[j];
A[j] = A[i];
A[i] = temp;
}
for (int i = 0; i < SIZE; i++) {
printf(" %d ", A[i]);
}
printf("\n");
}
if (select == j)
return A[j];
else if (select < j)
Selection(A, left, j - 1, select);//피봇보다 작은 그룹
else if (select > j)
Selection(A, j + 1, right, select);//피봇보다 큰 그룹
else
return -1;
}
}
int main() {
int n = SIZE;
int a[] = { 6,3,11,9,12,2,8,15,18,10,7,14 };
int k = 2;
printf("배열");
for (int i = 0; i < SIZE; i++) {
printf(" %d ", a[i]);
}
printf("\n");
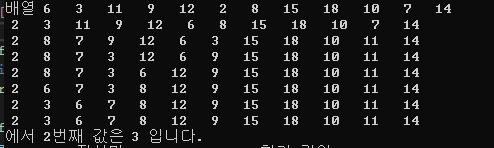
int result=Selection(a, 0, n - 1,k-1);
printf("에서 %d번째 값은 %d 입니다.",k,result);
return 0;
}
'강의내용 복습 > 컴퓨터 알고리즘' 카테고리의 다른 글
| Greedy 알고리즘 -Dijkstra 알고리즘 (0) | 2023.04.18 |
|---|---|
| Greedy 알고리즘 - Prim 알고리즘 (0) | 2023.04.16 |
| Greedy 알고리즘-거스름돈 문제, Kruskal MST (0) | 2023.04.09 |
| 분할 정복 알고리즘-merge sort (1) | 2023.03.21 |
| 컴퓨터 알고리즘- 알고리즘의 첫걸음 (0) | 2023.03.21 |
