분할 정복 알고리즘-merge sort
분할 정복 알고리즘이란?
-주어진 문제의 입력을 분할하여 문제를 해결하는 방식의 알고리즘.
->문제를 나누어서 풀면 더 효율적인 경우 사용
-대부분의 분할 정복 알고리즘은 분할만 해서는 해를 구할 수 없다.
-따라서 분할된 부분 문제들을 정복해야한다.
->부분해를 찾는다.
->일반적으로 부분 문제들의 해를 취합하여 보다 큰 부분 문제의 해를 구한다.
-종류
1.합병 정렬(merge sort)
합병 정렬은 입력이 2개의 부분문제로 분할되고, 부분문제의 크기가 1/2로 감소하는 분할 정복 알고리즘.
1)n개의 숫자들을 n/2개씩 2개의 부분 문제로 분할(Divide)
2)각각의 부분문제를 해결(Conquer)
3)재귀적으로 합병 정렬(Merging)
2.퀵 정렬(quick sort)
위와 반대로 정복 후 분할. 문제를 2개의 부분문제로 분할한다.
1)배열의 원소 하나를 피봇(pivot)삼고 기준
2)피봇보다 작은 숫자들은 왼쪽, 피봇보다 큰 숫자들은 오른쪽에 위치하도록 분할ㄹ
3)분할된 부분문제에 대해서도 위와 동일한 과정을 재귀적으로 수행하여 정렬
3.선택 정렬(selection)
1) 최대 원소 찾기
2) 최대 원소를 오른쪽 끝 원소와 교환
3) 오른쪽 끝 원소를 제외
4)1~3 과정을 하나의 원소가 남을때까지 반복
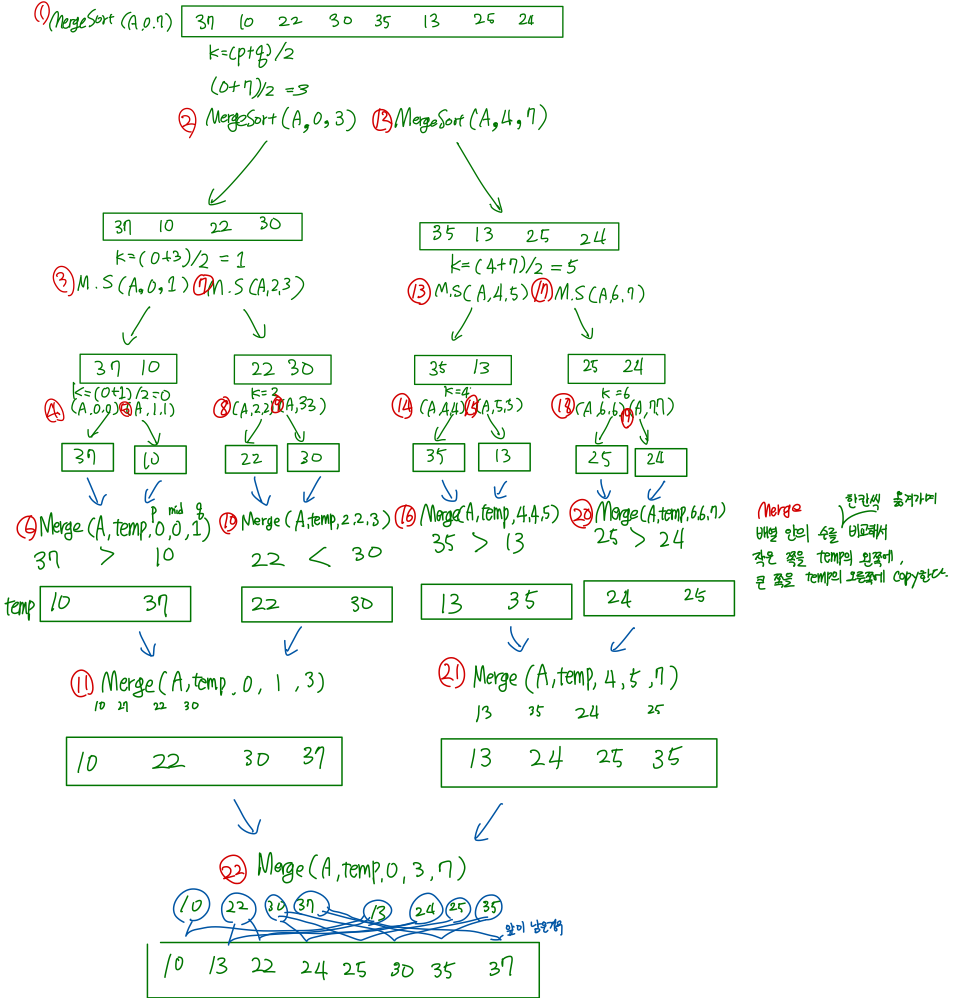
-합병 정렬 Pseudo Code
MergeSort(A,p,q)
입력:A[p]~A[q]
1. if (p<q){ //배열의 원소의 수가 2개 이상이면
2. k=(p+q)/2 //k: 반으로 나누기 위한 중간 원소의 인덱스
3. MergeSort(A,p,k) //앞부분 재귀 호출
4. MergeWort(A,k+1,q) //뒷부분 재귀 호출
5. A[p]~A[k]와 A[k+1]~A[q]를 합병한다.1. 정렬할 부분의 원소의 수가 2개 이상일 때에만 다음 단계 수행. 만일 n=1이면, 그 자체로 정렬된 것이므로 어떤 수행을 할 필요 없이 이전 호출했던 곳으로 리턴
2.정렬할 부분의 원소들을 1/2로 나누기 위해, k=(p+q)/2를 계산. 즉, 원소의 수가 홀수인 경우에는 k는 소수점 이하를 버림.
3~4. MergeSort(A,p,k)와 MergeSort(A,k+1,q)를 재귀 호출하여 각각 정렬
5.각각 정렬된 부분을 합병하고 합병 과정의 마지막에는 임시 배열에 있는 합병된 원소들을 배열 A로 복사. 즉 임시 배열 B[p]~B[q]를 A[p]~A[q]로 복사

-합병 정렬 Time Complexity
-분할하는 부분은 중간 인덱스 계산과 2번의 재귀 호출이므로 O(1)시간 소요
-합병의 수행 시간은 입력의 크기에 비례
-합병 정렬에서 수행되는 총 비교 횟수
:합병 복잡도*각 층에서 발생하는 복잡도
-합병 각 층을 살펴보면 모든 숫자가 합병에 참여. 합병은 입력 크기에 비례하므로, 각 층에서 수행된 비교 횟수는 O(n)

-소스코드
#include <stdio.h>
#include <stdlib.h>
#define SIZE 8
//merge과정에서는 배열 안의 값들을 temp로 copy해서 출력한다
//이 때, 배열 안의 수를 비교해서 작은 쪽을 temp의 왼쪽에, 큰 쪽을 temp의 오른쪽에 copy한다. A와 temp 인덱스에 주의한다.
void Merge(int A[], int temp[], int p, int mid, int q) {
int i, j, k, l;//k는 temp, ij는 인덱스
i = p;//A p에서부터 시작
j = mid + 1;
k = p;//temp p에서부터 시작
//합병
while (i <= mid && j <= q) {//왼쪽부터 중간까지 left, 중간부터 끝까지 right
if (A[i] <= A[j]) {//left가 right보다 작거나 같으면
temp[k++] = A[i++];//temp에 left copy 하고 temp위치 1증가
}
else {//left가 right보다 크면
temp[k++] = A[j++];//temp에 right copy 하고 mid,temp위치 1증가
}
}
//temp 위치에 적절한 부분만 카피함. 남아 있는 레코드의 일괄 복사
if (i > mid) {//뒤가 남은 경우
for (l = j; l <= q; l++) {
temp[k++] = A[l];
}
}
else {//앞이 남은 경우
for (l = i; l <= mid; l++) {
temp[k++] = A[l];//정렬하고 마지막으로 남은 값을 넣어주어야 하므로 앞이든 뒤든 마지막 인덱스 필요. i 혹은 j. p나 q 아님!!
}
}//정렬완료
for (l = p; l <= q; l++) {// temp로 정렬해서 복사한 값을 A에도 넣어준다.
A[l] = temp[l];
}
//temp를 출력해준다. 이 때, NULL부분은 출력하지 않는다.
for (int i = 0; i < l; i++) {
if (temp[i] != NULL)
printf(" %d ", temp[i]);
}
//NULL부분을 빼고 출력하게 되면 리스트 중 Merge단계에서 합병이 일어난 부분만 출력할 수 있다. temp에 들어간 부분 빼고 null이므로.
printf("\n");
}
void MergeSort(int A[], int p, int q) {
int temp[SIZE] = { NULL };
int k;
if (p < q) {//배열의 원소의 수가 2개 이상이면
k = (p + q) / 2;//반으로 나누기 위한 중간 원소의 인덱스
MergeSort(A, p, k);//왼쪽 나누기(앞부분 재귀 호출)
MergeSort(A, k + 1, q);//오른쪽 나누기(뒷부분 재귀 호출)
Merge(A, temp, p, k, q);//A[p]~A[k]와 A[k+1]~A[q]를 합병한다.
}
}
int main() {
int n = SIZE;
int a[] = { 37,10,22,30,35,13,25,24 };
printf("Before Sorting:");
for (int i = 0; i < SIZE; i++) {
printf(" %d ", a[i]);
}
printf("\n");
MergeSort(a, 0, n - 1);
printf("\nAfter Sorting: ");
for (int i = 0; i < SIZE; i++) {
printf(" %d ", a[i]);
}
return 0;
}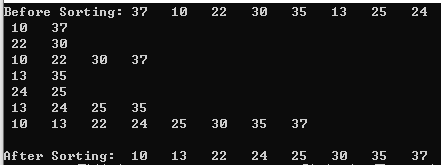
분할 ~합병
소스코드 전체 참고한 과정